Gas Laws

The behavior of gas under different pressures, volumes and temperatures have been widely studied in the history of Physics. In 1662, Robert Boyle discovered that close to room temperature and at about one atmospheric pressure, the pressure and volume of gases are inversely proportional to each other and this relationship became known as Boyle’s Law. Boyle's Law is written as

where the proportionality constant CB is NkT.

Jacques Charles discovered in 1780 that close to room temperature and at about one atmospheric pressure, the volume and temperature of gases are directly proportional to each other. Known today as Charles’s Law, which is written as 

where the proportionality constant CC is Nk/P.

The Gay-Lussac’s Law states that  close to room temperature and at about one atmospheric pressure, the pressure and temperature of gases are directly proportional to each other. It was discovered by Joseph Louis Gay-Lussac in 1809 and named after him. Gay-Lussac’s Law is written as 

where the proportionality constant CG = Nk/V.

These laws can be explained if we assume that the gas is ideal. The ideal gas model is used to describe the behavior of dilute gases at low pressures and high temperatures. Many gases e.g., nitrogen, oxygen and hydrogen, can be considered to be ideal gases at room temperature and pressures close to 1 atm. Using this assumption, combining the three gas laws discuss above, which is discovered experimentally gives as the equation of the state of an ideal gas.

where P is the pressure, V is the volume, N is the number of particles and T is the temperature of the gas measured in the absolute or Kelvin scale. The constant k in the ideal gas equation is called the Boltzmann constant and has the value k = 1.3806488×10−23 m^2·kg/s^2·K^1.

In this experiment, we wish to verify the Boyle's Law and Charles's Law only and  use the ideal gas equation to compute for the number of particles in the gas.

Boyle's Law

First, a beaker was filled with water up to 3/4 full and the water was boiled. The water was boiled throughout the activity. The air chamber can was then connected to the mass lifter apparatus using the rubber tubing. The air chamber can was then placed in the hot bath. The piston was lifted to its maximum height and the gas pressure sensor was connected to the Vernier LabQuest. The temperature T was monitored throughout the experiment. A 50 g standard mass was placed on the platform of the mass lifter apparatus and the height h of the piston and the pressure P was recorded. The previous step was also done for the 100,150,200 and 250 g masses.

The height of the gas in the piston where recorded. The volume of the cylinder Vcyl for each height was computed. The reciprocal P of each pressure reading was computed. Plotting  Vcyl vs P^-1 was done. 

Table B1

Table 1 above shows us that as we increase the mass of the object that we place, the height decreases and the pressure increases as well.

Figure 1

The information that we got from the linear fit equation are the following:

We obtain the volume of the chamber which is .0004 m^3, and also we can get the number of particle using the slope of the linear fit which is 1.0543E+22.

Charles's Law

The first step in this part of the experiment was to remove the beaker  (will serve as the hot bath) from the top of the stove. The air chamber was placed in the hot bath. The pressure P was monitored throughout the experiment. The temperature T of the hot bath was measured using a digital thermometer and the initial height h of the piston was recorded. 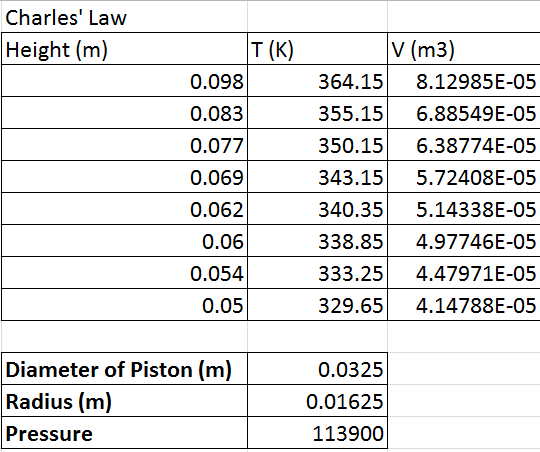Chunks of ice were slowly added on the hot bath while taking h and T measurements at equal time intervals. A graph of Vcham VS Temperature using the obtained data below. Also, the data from table 2 tells us that as the temperature decreased, the height decreased which means that the volume decreased.

Table 2A

Figure 2

Table 2B

 The number of particles N, which is 8.2487E+21 and the volume of the air chamber can Vcham is .0003 m^3 were calculated from the slope and y-intercept, respectively.

Conclusion: The data is precise because we have R^2 = .99 on both experiment. The data on the two experiment has only small discrepancy, since the theoretical number of particles is not given, the data obtained cannot be verified if its accurate. Over all, the experiment is well done with a small discrepancy.

Reference:

1.       “Experiment 9 Gas Laws,” Laboratory Manual for Physics (Physics 73.1), (2013)